캐글 타이타닉 탑승자 데이터를 기반으로 생존자 예측
Passengerid: 탑승자 데이터 일련번호survived: 생존 여부 (0:사망, 1:생존)pclass: 티켓의 선실 등급 (1:일등석, 2:이등석, 3:삼등석)sex: 탑승자 성별name: 탑승자 이름Age: 탑승자 나이sibsp: 같이 탑승한 형제자매 또는 배우자 인원수parch: 같이 탑승한 부모님 또는 어린이 인원수ticket: 티켓 번호fare: 요금cabin: 선실 번호embarked: 중간 정착 항구 (C:Cherbourg, Q:Queenstown, S:Southhampton)
1. 타이타닉 탑승자 파일 로딩
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
titanic_df = pd.read_csv('train.csv')
titanic_df.head(3)
데이터 column 타입 확인
print('\n ### train 데이터 정보 ### \n')
print(titanic_df.info())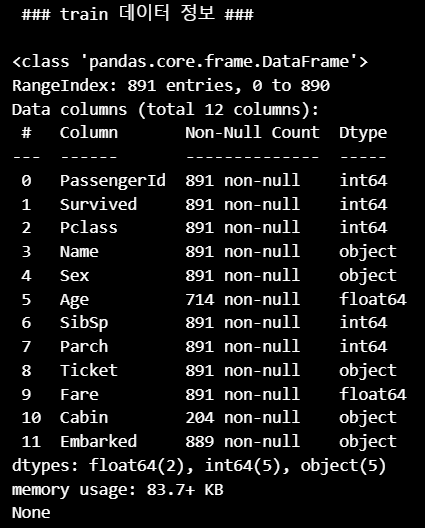
RangeIndex는 DataFrame 인덱스 범위를 나타내므로 전체 row 수를 알 수 있음- 현재 데이터는 891개 row로 구성되어 있음
- column 수는 12개
- 2개의 column이 float64
- 5개의 column이 int64
- 5개의 column이 object (판다스의 object 타입은
string타입으로 봐도 무방)
Age,Cabin,Embarked칼럼은 각각 714개, 204개, 889개의 Not Null 값을 가지고 있으므로 각각 117개, 608개, 2개의 Null 값(NaN)을 가지고 있음
2. Null 값 처리
Note
사이킷런 머신러닝 알고리즘은 Null 값을 허용하지 않으므로 Null 값을 어떻게 처리할지 결정해야 함
- 여기서는 DataFrame의
fillna()함수를 사용해 간단하게 Null 값을 평균 또는 고정 값으로 변경
titanic_df['Age'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())
titanic_df['Cabin'] = titanic_df['Cabin'].fillna('N')
titanic_df['Embarked'] = titanic_df['Embarked'].fillna('N')
print('데이터 세트 Null 값 갯수 ',titanic_df.isnull().sum().sum())
>>> 데이터 세트 Null 값 갯수 0Cabin과Embarded는 범주형 데이터로 결측치를 단순히 제거하거나 평균으로 대체할 수 없기 때문에 해당 값이 원래 없었다는 것을 명확히 하기 위하여 N으로 대체
3. 문자열 feature 확인
print(' Sex 값 분포 :\n',titanic_df['Sex'].value_counts())
print('\n Cabin 값 분포 :\n',titanic_df['Cabin'].value_counts())
print('\n Embarked 값 분포 :\n',titanic_df['Embarked'].value_counts())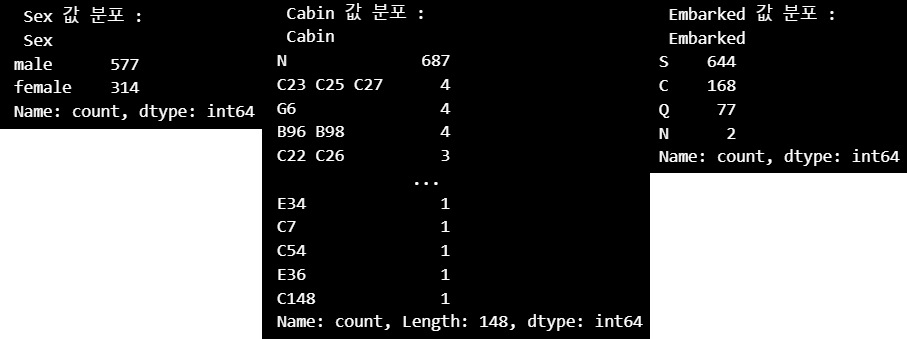
Sex,Embarked값은 별 문제가 없으나,Cabin(선실)의 경우 N이 687건으로 가장 많은 것도 특이하지만, 속성 값이 제대로 정리가 되지 않은 것처럼 보임C23 C25 C27과 같이 여러Cabin이 한꺼번에 표기된 값이 4건이나 되고,Cabin의 경우 선실 번호 중 선실 등급을 나타내는 첫 번째 알파벳이 중요해 보임
Tip
왜냐하면 이 시절에는 지금보다도 부자와 가난한 사람에 대한 차별이 더 있던 시절이었기에 일등실에 투숙한 사람이 삼등실에 투숙한 사람보다 더 살아날 확률이 높았을 것!
- 따라서
Cabin의 경우 앞 문자만 추출!
titanic_df['Cabin'] = titanic_df['Cabin'].str[:1]
print(titanic_df['Cabin'].head(3))
>>> 0 N
1 C
2 N
Name: Cabin, dtype: object4. 예측 수행 전 데이터 탐색
어떤 유형의 승객이 생존 확률이 높았을까?
Tip
바다에서 사고가 날 경우 여성과 아이들 그리고 노약자가 제일 먼저 구조 대상! 그리고 아마도 부자나 유명인이 다음 구조 대상이었을 것 예상컨데 삼등실에 탄 많은 가난한 이는 생존하지 못할 확률이 높을 것
a. 성별에 따른 생존자 수 비교
titanic_df.groupby(['Sex','Survived'])['Survived'].count()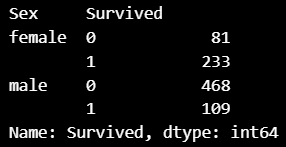
Survived칼럼은 label로서 결정 클래스 값- 탑승객은 남자가 577명, 여자가 314명으로 남자가 더 많았음
- 여자는 314명 중 233명으로 약 74.2%가 생존했지만, 남자의 경우에는 577명 중 468명이 죽고 109명만 살아남아 약 18.8%가 생존
- 그래프로 확인
sns.barplot(x='Sex', y='Survived', data=titanic_df) - 기본적인 작동 방식
x='Sex':Sex별로 그룹화 (male,female)y='Survived':Survived값의 평균 계산- 막대 높이 : 그룹별
Survived평균Survived컬럼은 0 또는 1이므로, 평균값이 곧 생존 확률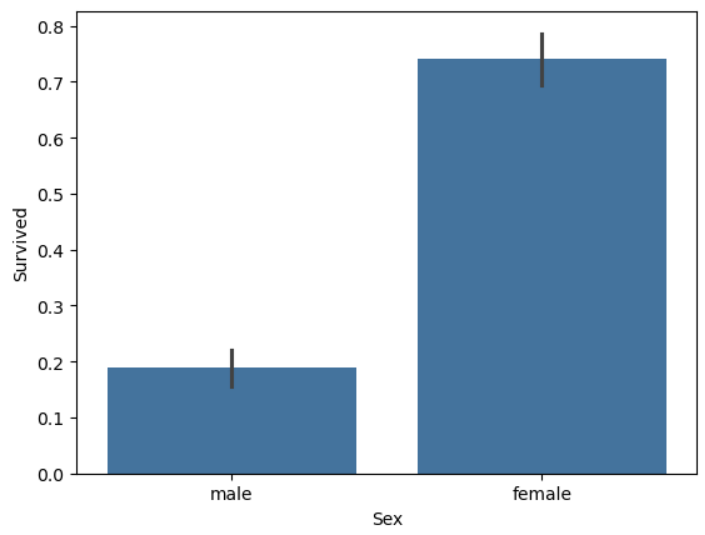
b. 부에 따른 생존자 수 비교 (feat. 성별)
- 부를 측정할 수 있는 속성으로 적당한 것은 객실 등급
- 객실 등급 별 성별에 따른 생존 확률 비교
sns.barplot(x='Pclass', y='Survived', hue='Sex', data=titanic_df)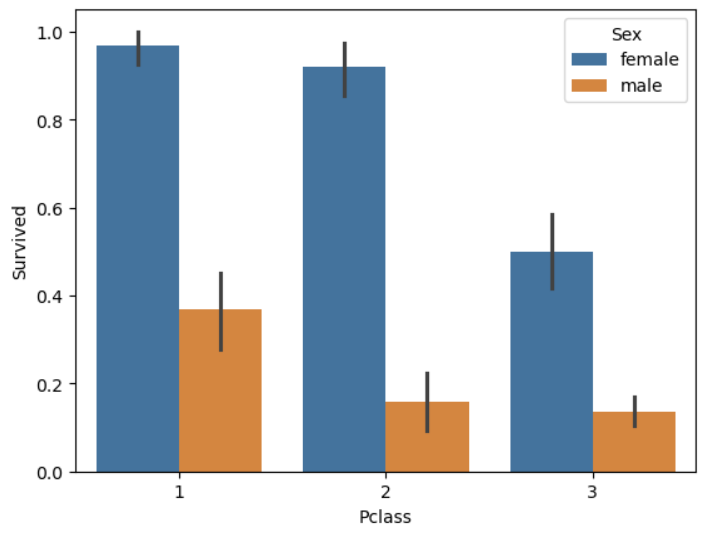
hue파라미터 : 데이터를 또 다른 기준으로 그룹화하여 색상별로 나누어 표현- 즉, 같은 x값에 대해 서브 그룹을 만들어서 여러 개의 막대를 나란히 표시하는 기능
- 여성의 경우 일, 이등실에 따른 생존 확률의 차이는 크지 않으나, 삼등실의 경우 생존 확률이 상대적으로 많이 떨어짐
- 남성의 경우 일등실의 생존 확률이 이, 삼등실의 생존 확률보다 월등히 높음
c. 나이에 따른 생존 확률
Tip
Age의 경우 값 종류가 많기 때문에 범위별로 분류해 카테고리 값 할당
- 0~5세 : Baby
- 6~12세 : Child
- 13~18세 : Teenager
- 19~25세 : Student
- 26~35세 : Yiung Adult
- 36~60세 : Adult
- 61세 이상 : Elderly
- -1 이하의 오류 값은 Unknown으로 분류
# 입력 age에 따라 구분값을 반환하는 함수 설정. DataFrame의 apply lambda식에 사용.
def get_category(age):
cat = ''
if age <= -1: cat = 'Unknown'
elif age <= 5: cat = 'Baby'
elif age <= 12: cat = 'Child'
elif age <= 18: cat = 'Teenager'
elif age <= 25: cat = 'Student'
elif age <= 35: cat = 'Young Adult'
elif age <= 60: cat = 'Adult'
else : cat = 'Elderly'
return cat
# 막대그래프의 크기 figure를 더 크게 설정
plt.figure(figsize=(10,6))
# X축의 값을 순차적으로 표시하기 위한 설정
group_names = ['Unknown', 'Baby', 'Child', 'Teenager', 'Student', 'Young Adult', 'Adult', 'Elderly']
# lambda 식에 위에서 생성한 get_category( ) 함수를 반환값으로 지정.
# get_category(X)는 입력값으로 'Age' 컬럼값을 받아서 해당하는 cat 반환
titanic_df['Age_cat'] = titanic_df['Age'].apply(lambda x : get_category(x))
sns.barplot(x='Age_cat', y = 'Survived', hue='Sex', data=titanic_df, order=group_names)
titanic_df.drop('Age_cat', axis=1, inplace=True)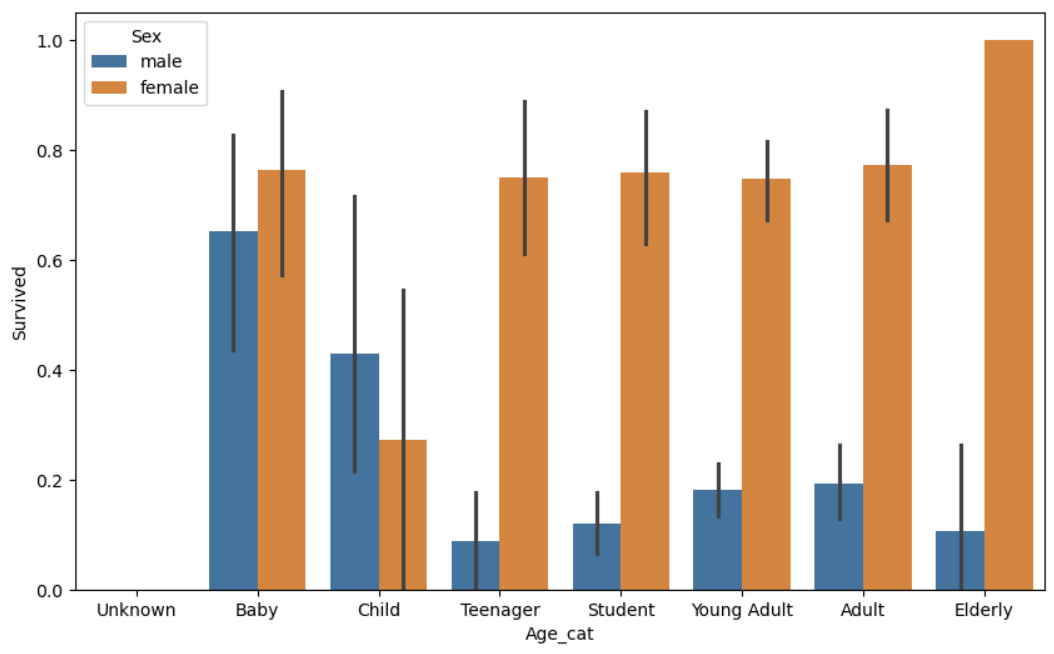
- 여자
Baby의 경우 비교적 생존 확률이 높았지만, 여자Child의 경우 다른 연령대에 비해 생존 확률이 낮음 - 여자
Elderly의 경우는 매우 생존 확률이 높았음
Summary
이제까지 분석한 결과
Sex,Age,PClass등이 중요하게 생존을 좌우하는 feature임을 어느 정도 확인 가능
5. 문자열 카테고리 feature를 숫자형으로 변환
Note
- 인코딩은 사이킷런의
LabelEncoder클래스를 이요해 레이블 인코딩 적용
- 레이블 인코딩은 각 범주를 정수형으로 변환하는 방식
LabelEncoder객체는 카테고리 값의 유형 수에 따라 0 ~ (카테고리 유형 수 -1)까지의 숫자 값으로 변환- 사이킷런의 전처리 모듈의 대부분 인코딩 API는 사이킷런의 기본 프레임워크 API인
fit(),transform()으로 데이터 변환
- 여러 칼럼을
encode_features()함수를 새로 생성해 한 번에 변환
from sklearn.preprocessing import LabelEncoder
def encode_features(dataDF):
features = ['Cabin', 'Sex', 'Embarked']
for feature in features:
le = LabelEncoder()
le = le.fit(dataDF[feature])
dataDF[feature] = le.transform(dataDF[feature])
return dataDF
titanic_df = encode_features(titanic_df)
titanic_df.head()
Sex,Cabin,Embarked속성이 숫자형으로 바뀜
6. 데이터 전처리를 수행하는 transform_features() 만들기
Note
지금까지 feature를 가공한 내역을 정리하고 이를 함수로 만들어 쉽게 재사용할 수 있도록 구성
transform_features()
- Null 처리, 불필요한 feature 제거, 인코딩을 수행하는 내부 함수로 구성
- 불필요한 feature 제거는
drop_features(df)로 수행하며 머신러닝 알고리즘에 불필요한, 단순한 식별자 수준의 feature인PassengerId,Name,Ticketfeature 제거
from sklearn.preprocessing import LabelEncoder
# Null 처리 함수
def fillna(df):
df['Age'] = df['Age'].fillna(df['Age'].mean())
df['Cabin'] = df['Cabin'].fillna('N')
df['Embarked'] = df['Embarked'].fillna('N')
df['Fare'] = df['Fare'].fillna(0)
return df
# 머신러닝 알고리즘에 불필요한 피처 제거
def drop_features(df):
df.drop(['PassengerId', 'Name', 'Ticket'], axis=1, inplace=True)
return df
# 레이블 인코딩 수행.
def format_features(df):
df['Cabin'] = df['Cabin'].str[:1]
features = ['Cabin', 'Sex', 'Embarked']
for feature in features:
le = LabelEncoder()
le = le.fit(df[feature])
df[feature] = le.transform(df[feature])
return df
# 앞에서 설정한 데이터 전처리 함수 호출
def transform_features(df):
df = fillna(df)
df = drop_features(df)
df = format_features(df)
return df7. 학습 및 예측 준비
Todo
- 원본 CSV 파일을 다시 로딩하고 label 값인
Survived속성만 별도 분리해 클래스 결정값 데이터 세트로 만들기- 그리고
Survived속성을 drop 해 feature 데이터 세트 만들기- 이렇게 생성된 feature 데이터 세트에
transform_features()를 적용해 데이터 가공
# 원본 데이터를 재로딩 하고, feature데이터 셋과 Label 데이터 셋 추출.
titanic_df = pd.read_csv('train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived',axis=1)
X_titanic_df = transform_features(X_titanic_df)- 내려받은 학습 데이터 세트를 기반으로
train_test_split()를 이용해 별도의 테스트 데이터 세트 추출 - 테스트 데이터 세트 크기는 전체의 20%
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test=train_test_split(X_titanic_df, y_titanic_df,
test_size=0.2, random_state=11)8. 학습 및 예측
Note
ML 알고리즘인 결정 트리, 랜덤 포레스트, 로지스틱 회귀를 이용해 타이타닉 생존자 예측 여기서는 사이킷런 기반의 머신러닝 코드에 익숙해지는 것을 목표!
- 결정 트리 :
DecisionTreeClassifier- 랜덤 포레스트 :
RandomForestClassifier- 로지스틱 회귀 :
LogisticRegression핵심 과정
- 사이킷런 클래스를 이용해
train_test_split()으로 분리한 학습 데이터와 테스트 데이터를 기반으로 머신러닝 모델을 학습하고(fit), 에측(predict)- 예측 성능 평가는 정확도로 할 것이며 이를 위해
accuracy_score()API 사용
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 결정트리, Random Forest, 로지스틱 회귀를 위한 사이킷런 Classifier 클래스 생성
dt_clf = DecisionTreeClassifier(random_state=11)
rf_clf = RandomForestClassifier(random_state=11)
lr_clf = LogisticRegression(solver='liblinear')
# DecisionTreeClassifier 학습/예측/평가
dt_clf.fit(X_train , y_train)
dt_pred = dt_clf.predict(X_test)
print('DecisionTreeClassifier 정확도: {0:.4f}'.format(accuracy_score(y_test, dt_pred)))
# RandomForestClassifier 학습/예측/평가
rf_clf.fit(X_train , y_train)
rf_pred = rf_clf.predict(X_test)
print('RandomForestClassifier 정확도:{0:.4f}'.format(accuracy_score(y_test, rf_pred)))
# LogisticRegression 학습/예측/평가
lr_clf.fit(X_train , y_train)
lr_pred = lr_clf.predict(X_test)
print('LogisticRegression 정확도: {0:.4f}'.format(accuracy_score(y_test, lr_pred)))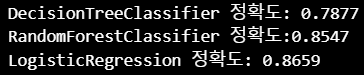
- 3개의 알고리즘 중
LogisticRegression이 타 알고리즘에 비해 높은 정확도를 나타내고 있음 - 하지만 아직 최적화 작업을 수행하지 않았고, 데이터 양도 충분하지 않기 때문에 어떤 알고리즘이 가장 성능이 좋다고 평가할 수는 없음
교차 검증으로 결정 트리 모델 평가
Note
사이킷런
model_selection패키지의KFold클래스,cross_val_score(),GridSearchCV클래스를 모두 사용!
a. KFold 클래스를 이용한 교차검증
- fold 개수는 5개로 설정
from sklearn.model_selection import KFold
def exec_kfold(clf, folds=5):
# 폴드 세트를 5개인 KFold객체를 생성, 폴드 수만큼 예측결과 저장을 위한 리스트 객체 생성.
kfold = KFold(n_splits=folds)
scores = []
# KFold 교차 검증 수행.
for iter_count , (train_index, test_index) in enumerate(kfold.split(X_titanic_df)):
# X_titanic_df 데이터에서 교차 검증별로 학습과 검증 데이터를 가리키는 index 생성
X_train, X_test = X_titanic_df.values[train_index],
X_titanic_df.values[test_index]
y_train, y_test = y_titanic_df.values[train_index],
y_titanic_df.values[test_index]
# Classifier 학습, 예측, 정확도 계산
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
accuracy = accuracy_score(y_test, predictions)
scores.append(accuracy)
print("교차 검증 {0} 정확도: {1:.4f}".format(iter_count, accuracy))
# 5개 fold에서의 평균 정확도 계산.
mean_score = np.mean(scores)
print("평균 정확도: {0:.4f}".format(mean_score))
# exec_kfold 호출
exec_kfold(dt_clf , folds=5)
enumerate()반복(iterable) 객체를 순회할 때, 현재 몇 번째 반복인지(index)를 함께 반환하는 내장 함수
- 평균 정확도는 약 78.23%
b. cross_val_score() API를 이용한 교차검증
from sklearn.model_selection import cross_val_score
scores = cross_val_score(dt_clf, X_titanic_df, y_titanic_df, cv=5)
for iter_count, accuracy in enumerate(scores):
print("교차 검증 {0} 정확도: {1:.4f}".format(iter_count, accuracy))
print("평균 정확도: {0:.4f}".format(np.mean(scores)))
cross_val_score()와 방금 전 k fold의 평균 정확도는 왜 다를까?
cross_val_score()가StratifiedKFold를 이용해 fold 세트를 분할하기 때문!
c. GridSearchCV를 이용한 예측 성능 측정
from sklearn.model_selection import GridSearchCV
parameters = {'max_depth':[2,3,5,10],
'min_samples_split':[2,3,5], 'min_samples_leaf':[1,5,8]}
grid_dclf = GridSearchCV(dt_clf , param_grid=parameters , scoring='accuracy' , cv=5)
grid_dclf.fit(X_train , y_train)
print('GridSearchCV 최적 하이퍼 파라미터 :',grid_dclf.best_params_)
print('GridSearchCV 최고 정확도: {0:.4f}'.format(grid_dclf.best_score_))
best_dclf = grid_dclf.best_estimator_
# GridSearchCV의 최적 하이퍼 파라미터로 학습된 Estimator로 예측 및 평가 수행.
dpredictions = best_dclf.predict(X_test)
accuracy = accuracy_score(y_test , dpredictions)
print('테스트 세트에서의 DecisionTreeClassifier 정확도 : {0:.4f}'.format(accuracy))
- 최적화된 하이퍼 파라미터인
max_depth=3, min_samples_leaf=5, min_samples_split=2로DecisionTreeClassifier를 학습시킨 뒤 예측 정확도가 약 87.15%로 향상됨 - 하지만, 일반적으로 하이퍼 파라미터를 튜닝하더라도 이 정도 수준으로 증가하기는 매우 어려움
- 테스트용 데이터 세트가 작기 때문에 수치상으로 예측 성능이 많이 증가한 것처럼 보임